转载:原始链接:[http://jayxv.github.io/2019/11/11/密码学学习笔记之浅析Pollard's rho algorithm及其应用/](https://jayxv.github.io/2019/11/11/密码学学习笔记之浅析Pollard's rho algorithm及其应用/)
已经小半年没学密码了,其实以后更想往渗透方向走,但密码没学好还是挺遗憾的。昨天刚好收到了山石安研院 暑期CTF crypto 训练营的录取邮件。既惊讶又欣喜,当时报名参加的时候是想着投着试一下,并没有报希望进去的。填CTF学习意向方向时,本想着去跟着大佬学习下web安全,但看了下都是 java,php安全的更多,感觉不太适合,又看到了密码。想了下还是继续干老本行,学习密码方向。
密码学习看的V神的blog,密码学学习笔记之浅析Pollard's rho algorithm及其应用
以下做的笔记也仅供学习,作为学习笔记,因为V神总结的太好了,所以很多我基本照搬过来了,有些代码和解释做了些改动。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
from Crypto.Util.number import getPrime, isPrime
flag = 'BCNS{***************}'
nbits = 2048
gbits = 1000
g = getPrime(int(gbits))
while True:
a = getPrime(int(nbits * 0.5) - gbits)
p = 2 * g * a + 1
if isPrime(p):
break
while True:
b = getPrime(int(nbits * 0.5) - gbits)
q = 2 * g * b + 1
if p != q and isPrime(q):
break
N = p * q
e = 65537
def str2int(s):
return int(s.encode('hex'), 16)
with open('pubkey.txt', 'w') as f:
f.write(str(e) + '\n')
f.write(str(N) + '\n')
plain = str2int(flag)
c = pow(plain, e, N)
with open('cipher.txt', 'w') as f:
f.write(hex(c))
|
文献:Further Attacks on Server-Aided RSA Cryptosystems
对服务器上的RSA加密系统的进一步攻击,Further Attacks on Server-Aided RSA Cryptosystems解决的是大数分解的一个问题
$N=p*q(N>512bit)$,其中$(p-1)$ 和 $(q-1)$有一个大的公因数 $β$ ,并且 $p(bit) = q(bit) = \frac{1}{2} N(bit)$
即原文中提及的 $p$ and $q$ are both of order $N^\frac{1}{2}$
在 Further Attacks on Server-Aided RSA Cryptosystems 的第一个攻击阶段中提到: 利用 Pollard’s ρ methods ,其中用于取伪随机值的maps函数为 $g(x)=$ $x^{N−1}$ $+$ $3$ $(mod$ $N)$ , 这将在时间复杂度为 $O($ $\sqrt {p/β}$ $)$ 内分解 $N$ ,因为在 $x^{N-1}$ $(mod$ $p)$ 中,最多有 $(p-1)/β$ $+$ $1$个值。
当 $β$ 超过 150bits 时,$\sqrt {p/β}$ ~ $2^{53}$ ,N 是易受到攻击的。

Pollard's rho algorithm
波拉德的 ρ 算法是整数分解的一种算法。 它是约翰 · 波拉德在1975年发明的。 它只占用了很少的空间,并且它的预期运行时间与被分解的合数的最小质因数大小的平方根成正比
假设我们需要分解$n$ ,$n=q∗p$ ,其中 $q$ 为 $n$ 的非平凡因子 $($即 $q$ 不等于 $1$ 或 $n)$。
我们需要一个模 $n$ 的多项式,例如:$g(x)≡$ $x^2$ $+$ $1$ $(mod$ $n)$ ,用于生成“伪随机”数列。我们选择一个起始值
例如,2,即 $x_1=g(2),x_2=g(g(2)),x_3=g(g(g(2)))……$
这里值得注意的是,这个数列是有限的,由于生日问题,序列 $x_k$ mod $(n)$ 最终会重复,一旦一个序列由重复的值,这个序列就会循环,因为每个值依赖于它之前的值, 这种最终循环的结构产生了“ ρ 算法”的名称
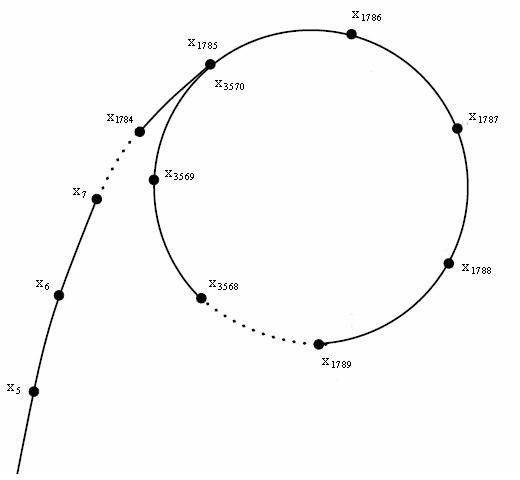
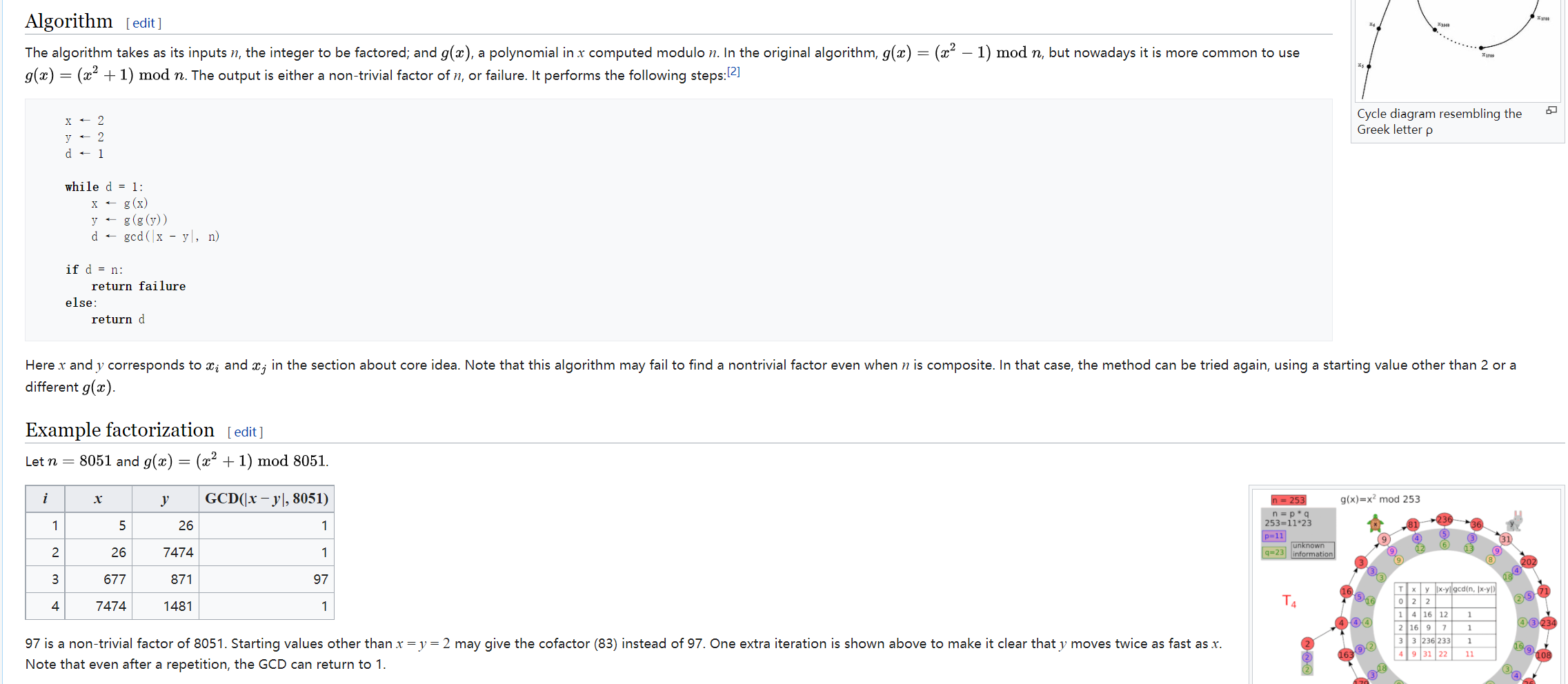
该算法将要因式分解的整数作为输入 N,和 $g(x),x$ 计算模 N 的多项式。在原始算法中, $g(x) = (x^2$ $-$ $1)$ $mod$ $n$ ,但现在更为常见的是使 $g(x) = (x^2$ $+$ $1)$ $mod$ $n$ 用 ,输出的要么是 n 的重要因子,要么失败。
这里我们可以举一个简单的小例子,我们设 $n$ 为640,$g(x)=x^2$,$x$ 起始值为2,
1
2
3
4
|
b=2
while True:
b *= 2
print(b%640)
|
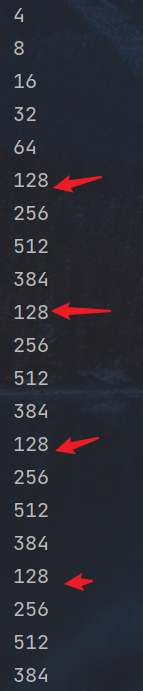
我们可以看到,128为这个取模多项式的循环节点,
回到话题,这里继续用 Floyd’s cycle-finding algorithm发现:设立两个节点,$i,j$,在每一步中,$i$ 每次移动一个节点,$j$ 每次移动两个节点,然后检查 $gcd(x_i−x_j,n)$ 是否 $≠1$,如果不等于,那么 $gcd$ 的结果便是 $p$ 。并且,这也意味着序列 $x_k$ $(mod$ $p)$ 也会重复。这是因为,如果 $x_i≡x_j(mod$ $p)$ ,那么 $x_i$ 与 $x_j$ 之间的差必然是 $p$ 的倍数。同时,这也说明,$gcd(x_i−x_j,n)$ 不等于 1 的结果无论如何最终都会到来,但是可能是 $n$ 自己,此时,代表 Pollard’s ρ algorithm 失败了,可以使用不同的起始值,再次运算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
def gcd(a, b):
while b:
a, b = b, a%b
return a
def mapx(x):
x=(x*x+1)%n
return x
def pollard_rho (x1,x2):
while True:
x1=mapx(x1)
x2=mapx(mapx(x2))
p=gcd(x1-x2,n)
if (p == n):
print "fail"
return
elif (p!=1):
print("p: "+str(p))
print("q: "+str(n/p))
break
|
1980年,Richard Brent 发表了 rho 算法的一个更快的变体。 他使用了与 Pollard 相同的核心思想,但是使用了不同的循环检测方法,用相关的 Brent’s cycle finding method 取代了 Floyd’s cycle-finding algorithm
他观察到,如果 $gcd(a,n) > 1$,那么 $gcd(a∗b,n) > 1$(b为任意正整数)。所以,取代 Floyd’s cycle-finding algorithm 的每一步都检查 $gcd(a,n)$ ,他定义了一个 $z$,$z=(x_2−x_3·(x_3−x_5……(x_{101}−x_{201}(mod$ $n)$ 即每一百步才检查一次 $gcd(x_i−x_j,n)$,这么作主要是为了加速结果。 但有时它可能会引入重复因子导致算法失败,例如当 $n$ 是一个正方形时。 但是这样使用常规算法就好了。
那么回过头来我们解最初出现的那一道题,题中,p−1和 q−1 有很明显的公因子 2*g ,于是根据 Further Attacks on Server-Aided RSA Cryptosystems 中 The first stage of the attack 所提到的,
为了分解N ,我们只需要运用 Pollard’s ρ algorithm,其中用于生成“伪随机”数列的多项式为:$g(x)=(x^{n−1}+3)$ % $n$
python代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
def gcd(a, b):
while b:
a, b = b, a%b
return a
def mapx(x):
x=(pow(x,n-1,n)+3)%n #pow(x,n-1,n)是为了减小数值,加速运算,
return x
def pollard_rho (x1,x2):
while True:
x1=mapx(x1)
x2=mapx(mapx(x2))
p=gcd(x1-x2,n)
if (p == n):
print "fail"
return
elif (p!=1):
print("p: "+str(p))
print("q: "+str(n/p))
break
def main():
pollard_rho(1,1)
return
n= #题目所给
main()
|
很快就得到了分解结果:
1
2
|
p: 269650264692548566978074112284374842610174290139820885265484504337289566793938597346602155739081086557351072223620265806722570840534100033154119094965205722815997832769233104488619168771901129055476955760285445455863002454889900213302562844531316706652494637209760008084725213305051233367795241684697449224567
q: 258276228412453952342761280836395825062923086530462077126283048578424505488433072066288731568478598067378323835988126921525549266401826429976089921447823957120012574328943338611748836455846904031487340120916131749573015449886849838628971796160792125197442011286309182844265325360886052171423731486172590665747
|
题目:
1
2
3
4
5
6
7
8
9
|
from Crypto.Util.number import *
flag='XXXXXXXXXX'
e=0x10001
n=3464115689260819392935656139231271022088014497600959975252672820761470484618617542699739764705620767566046150296286140279466041905437740736319886548924058066340624280173573039937440574809212831672936265975209972857747738693288788052694888593629820783280181774594890101819911390468376042288685444703477639361249422054925155575158181408046447773183467474182159096249846479461475003039637685547191529769071424947165685996675043741359728960138725130116665515880652680244470002603320184043266997163009799067135481330853926800023087208636366543210276325733789567957712475079676808820490428973148590780103404729397985019089646026534758042652163974037179260930147000267787012874887703048185189387666199961350969478997330352491403611551096779887936063702892671572230523920277869824082318417366635732798078805070773662305098133013800559413976855639167085996705265872418286939474978058429877355305699191892248323534097124680592084808397263288943661630283254265898940430505371463275516870915261799702701453110383723660477322192658118815861974573497885759332587457883589126213868868281682733732394640188383458580555618181208722172011645063817887462511925363883111475043389367021569982583145912277082528397480756465818166640691294267829613428532584923122279261412957652411789780285394451850006055483598427256129336822790446219260722224551892755568723667049099823707012236618539013908897459508493477299241358343681962043777720375898238069411747593247677719659288861028038609681592049271388766040068274682329498410270047730060645409396168652996740411436504098243588534151795927613112273405281530700440843961363083171583053608594479571127638861391879160062136043924515492933057094406001740725150570943724333872057035272515676895138632004436149126542560186729495087753846670118167613304943153665660470977150177815354160112481310498255965933157902965011317272734556307544837058247794721427834401390455487872367113056168812990496943458920406382650794656884209032284257748450399719067686010156664485086500184078244358783696803659745365860507822269113477617988541658390715640119076036723560146145256418191555730429
m=bytes_to_long(flag)
c=pow(m,e,n)
# print(c)
assert c==1348180992713820685594359831085361247035354818267759694375727771380213764105201303900290589048476671838784929302557807429509301123621642066527762448168417430350203900517746161928291953862336621873868684964993481406952303460424386080800907869577832154132021624995347121475139439850224598911049824567475034545196149320206620924509546294914370633958171840525667753751028800452370972967842349036965813468093121305475860652163573748880159896028384459277781803606279654121781761535513864212749202340439422384362197321739535686506006254445152569135807838677803047115947240251817017395748631234023225248868640103807357800695487118067385969130665294711887439861169737031598274672286881054564295019370600398079829687943670066246766386800967129670975899437309257181151390273864539453238400821713398980792443187238155205199387468000884390778225928491109565539772444103430764411852162036780535068932010631521096301305200494731040799554079996593223419379540630567412342494359961515157700054387356888773321804429041668331430841954949061238002355270616266853430676140296078177898764114420743905073496118755793091902224563802923183897542996809393707165837427396760691616506592877656939455806776333105152244073459704842848097376929745632888315642056267589901527329593161439752243318158600747713335265681764274061086952626629147275106502354039293870614872849851780761537660716667003562253735923584765118319171207551032289722689929226947535724389015974764265109970513715649126340709399701638880824570967389428525179746112494690443526404899052482884526335312491500994658519105204100875596292743155076199283666094556235485722975240358390560161706163569618302627055238860096406627340558428533728688904747040262153892623865784320600845613247625784683300197845026108394831724602330903266980995146046956218083954561639114586880305451066793209385702886944430548686040360906088479432852330611586273784509957389880104225534635731572089138568407411433675077699382999593384336070450058824669351046095205147266720901917218217564113964074957585348227506587531149811564371155522575778721899999227020238022970334707476977210019
|
题目只给了 n,e,c 三个值,很显然要分解 N 得到 $p$ 和 $q$ ,其中的 N有 6048bits ,不可能直接分解了。
这里的 N 很大,显然不可能只有 p,q 两个因数,所以我们猜测 $N$ 是由若干个小素数的乘积得到的。
这里用到 Pollard’s ρ algorithm 来分解 N ,前面提到它的预期运行时间与被分解的合数的最小质因数大小的平方根成正比
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
import gmpy2
def mapx(x):
x = (x*x+1) % n
return x
def pollard_rho(x1,x2):
while 1:
x1 = mapx(x1)
x2 = mapx(mapx(x2))
d = gmpy2.gcd(x1-x2,n)
if d == n:
print("fail")
elif (d != 1):
return d
n = 3464115689260819392935656139231271022088014497600959975252672820761470484618617542699739764705620767566046150296286140279466041905437740736319886548924058066340624280173573039937440574809212831672936265975209972857747738693288788052694888593629820783280181774594890101819911390468376042288685444703477639361249422054925155575158181408046447773183467474182159096249846479461475003039637685547191529769071424947165685996675043741359728960138725130116665515880652680244470002603320184043266997163009799067135481330853926800023087208636366543210276325733789567957712475079676808820490428973148590780103404729397985019089646026534758042652163974037179260930147000267787012874887703048185189387666199961350969478997330352491403611551096779887936063702892671572230523920277869824082318417366635732798078805070773662305098133013800559413976855639167085996705265872418286939474978058429877355305699191892248323534097124680592084808397263288943661630283254265898940430505371463275516870915261799702701453110383723660477322192658118815861974573497885759332587457883589126213868868281682733732394640188383458580555618181208722172011645063817887462511925363883111475043389367021569982583145912277082528397480756465818166640691294267829613428532584923122279261412957652411789780285394451850006055483598427256129336822790446219260722224551892755568723667049099823707012236618539013908897459508493477299241358343681962043777720375898238069411747593247677719659288861028038609681592049271388766040068274682329498410270047730060645409396168652996740411436504098243588534151795927613112273405281530700440843961363083171583053608594479571127638861391879160062136043924515492933057094406001740725150570943724333872057035272515676895138632004436149126542560186729495087753846670118167613304943153665660470977150177815354160112481310498255965933157902965011317272734556307544837058247794721427834401390455487872367113056168812990496943458920406382650794656884209032284257748450399719067686010156664485086500184078244358783696803659745365860507822269113477617988541658390715640119076036723560146145256418191555730429
while (n!=1):
p = pollard_rho(2,2)
print(p)
n = n//p
|
跑半个小时得到6个:740160703366837, bits = 50
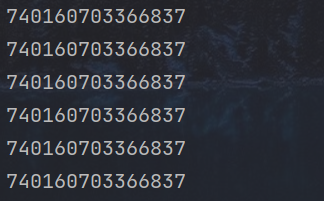
跑了几个小时后得到的结果:

flag 大小应该不是特别大,所以 740160703366837的六次方,bits = 50x6 = 300bits,用作新的 N 值来计算 flag ,应该足够了。
exp:
1
2
3
4
5
6
7
8
9
10
11
12
|
from gmpy2 import *
from libnum import *
p = 740160703366837
if is_prime(p):
n = pow(p,6)
e = 0x10001
c = 1348180992713820685594359831085361247035354818267759694375727771380213764105201303900290589048476671838784929302557807429509301123621642066527762448168417430350203900517746161928291953862336621873868684964993481406952303460424386080800907869577832154132021624995347121475139439850224598911049824567475034545196149320206620924509546294914370633958171840525667753751028800452370972967842349036965813468093121305475860652163573748880159896028384459277781803606279654121781761535513864212749202340439422384362197321739535686506006254445152569135807838677803047115947240251817017395748631234023225248868640103807357800695487118067385969130665294711887439861169737031598274672286881054564295019370600398079829687943670066246766386800967129670975899437309257181151390273864539453238400821713398980792443187238155205199387468000884390778225928491109565539772444103430764411852162036780535068932010631521096301305200494731040799554079996593223419379540630567412342494359961515157700054387356888773321804429041668331430841954949061238002355270616266853430676140296078177898764114420743905073496118755793091902224563802923183897542996809393707165837427396760691616506592877656939455806776333105152244073459704842848097376929745632888315642056267589901527329593161439752243318158600747713335265681764274061086952626629147275106502354039293870614872849851780761537660716667003562253735923584765118319171207551032289722689929226947535724389015974764265109970513715649126340709399701638880824570967389428525179746112494690443526404899052482884526335312491500994658519105204100875596292743155076199283666094556235485722975240358390560161706163569618302627055238860096406627340558428533728688904747040262153892623865784320600845613247625784683300197845026108394831724602330903266980995146046956218083954561639114586880305451066793209385702886944430548686040360906088479432852330611586273784509957389880104225534635731572089138568407411433675077699382999593384336070450058824669351046095205147266720901917218217564113964074957585348227506587531149811564371155522575778721899999227020238022970334707476977210019
phi = (p-1)*(p**5)
d = invert(e,phi)
m = pow(c,d,n)
print(n2s(m))
|
flag{G0oDJ0b_S0_SimPle_ChaMd5}
这里相当于我们直接把原题的 $n$ 给纂改了,
但为啥这里我们可以直接改 $n$ 呢?
这里再回顾一下基础知识好了
以下是 $M≡C^d (mod$ $N)$ 的证明:

求证的条件(设新的n值为小写n,原值为N ): 首先 $m < N$ ,所以 n > m 即可
其次,由于 n | N,所以 $ C = m^e$ $(mod$ $n)$
推理如下:
$N=$ $n * x$
$C = m^e$ $(mod$ $N)$
$m^e =$ $k*N$ $+$ $C$
==> $m^e =$ $knx$ $+$ $C$
==> $ C = m^e$ $(mod$ $n)$
所以只要新的 $n$ 满足, $m < n$, $C ≡ m^e$ $(mod$ $n)$ ,并且 $gcd(e,phi(n))=1$ ,即可解出 m 的值来
而一般情况下$n=p∗q$,所以基本不给你篡改 $n$ 的机会~
今天学习了
Further Attacks on Server-Aided RSA Cryptosystems,
Pollard’s ρ algorithm,
$M≡C^d (mod$ $N)$ 的证明。
看完之后,感觉基本上理解了,但是更底层的逻辑还待去思考。
看 V 神的blog学习感觉真好,写的很详细,通俗易懂,不懂的就问 V 神。最后,感谢 V神 的指导。






